Matching string prefixes using a prefix-trie 2
After discussion the general problem of matching string prefixes two weeks ago, we starting on the implementation of a prefix-trie to solve the problem efficiently last week.
Our implementation so far is able to quickly construct a prefix-trie from a list of strings. What is still missing is any kind of functionality to query the data structure for information.
Today we will take a look at how to use this data structure to enumerate all strings with a given prefix, and how to obtain the longest common prefix in that list.
Quick recap
Let us quickly remember what a prefix-trie is, and how we implemented it.
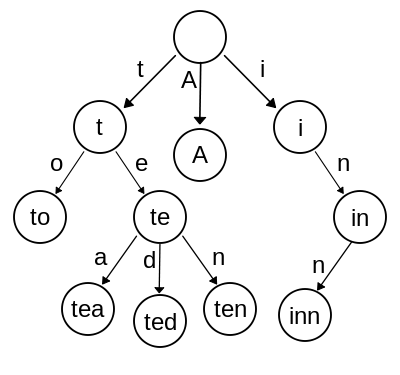
As you can see in this example diagram, a prefix-trie is a tree, where each edge or arc represents a character, and each node represents a string. The root is the empty string, and each other node is the string composed of the characters on the arcs from the root to the node.
Some nodes – including all leaves – are flagged to represent words, or members of our input string collection.
We implemented this data structure using a single class to represent nodes. Each node has a string property of the value it contains, which is null if the node is no valid value and simply represents a prefix. Further, each node contains a dictionary from characters to nodes. This represents the outgoing arcs and the respective children of the node. A leaf of our trie does not have a dictionary and the respective property is null instead.
In code, this is what we have to work with:
class Node
{
private readonly string value;
private readonly Dictionary<char, Node> children;
}If you are interested in how we build the prefix-trie data structure from a simple list of strings, make sure to read last week’s post where we design and implement the algorithm step by step.
Getting node with a given prefix
A prerequisite for the actual methods we are interested in is the ability to get a node that represents a given prefix.
This can be done fairly easily by starting with the root and then following the arcs of the trie according to the characters in the prefix.
We can implement this algorithm either recursively, or iteratively. In code:
Recursively:
Node getNode(string prefix)
{
return this.getNode(prefix, 0);
}
Node getNode(string prefix, int index)
{
if (index == prefix.Length)
return this; // node for prefix found
Node child;
if (!this.children.TryGet(prefix[index], out child))
return null; // no node found, invalid prefix
return child.getNode(prefix, index + 1);
}Iteratively:
Node getNode(string prefix)
{
var node = this;
foreach (var character in prefix)
{
if (!node.children.TryGet(character, out node))
return null; // no node found, invalid prefix
}
return node;
}Recursion often results in more elegant solutions than iteration. In this case I quite like both solutions, and leave it up to you which you prefer.
Personally, I would most likely go for the iterative approach, since it is both shorter, and more importantly easier on our stack. That being said, the compiler might very well be smart enough to detect the tail recursion and might then optimise by compiling to iterative machine code.
No matter which approach we take however, with this method in place we are now equipped now tackle our real questions.
All strings with prefix
Implementing a method that returns all strings starting with a given prefix is now almost trivial – almost.
We first use our previous method to get the node that represents the prefix, and then simple have to enumerate all values in the sub-trie of which this node is the root.
That enumeration however is not necessarily trivial.
A recursive approach would be implemented something like this – in pseudo code:
enumerateAllValues()
{
if (this.value != null)
enumerate this.value
if(this.children == null)
return
foreach (child in this.children)
child.enumerateAllValues()
}And in fact we can implement this as follows:
IEnumerable<string> enumerateAllValues()
{
if (this.value != null)
yield return this.value;
if(this.children == null)
yield break;
foreach (var s in this.children.Values
.SelectMany(c => c.enumerateAllValues())
)
yield return s;
}This works fine. But there is one caveat.
Notice how we have to flatten the collections returned by each node’s children using SelectMany, and how we then enumerate the entire result again simply so that in the end we end up with a single IEnumerable.
Maybe this is efficient enough for some, but I would like to improve our solution and get rid of the many-fold stacked yield returns.
Better enumeration
One thing we could do is enumerate all values into a list, instead of trying to return them lazily, and then returning the entire list.
IEnumerable<string> enumerateAllValues()
{
var list = new List<string>();
this.enumerateTo(list);
return list;
}
void enumerateTo(List<string> list)
{
if (this.value != null)
list.Add(this.value);
if(this.children == null)
yield break;
foreach (var child in this.children.Values)
child.enumerateTo(list);
}I consider this a much cleaner approach.
However, it came at a large cost: Notice how we construct the entire output before we return it. Depending on what we want to do with the results, this might need an unnecessary amount of space, and maybe we do not even care to enumerate the entire result in the first place.
In either case our solution would benefit from deferred execution. But can we add this without going back to our stacked yield returns?
Yes we can, by taking an iterative approach.
Instead of representing the moving through the tree using our implicit recursive calls, we will now navigate to other nodes explicitly in a loop. To make sure we do not lose track of where we are in the tree – which is easily possible since nodes do not know their parents – we need to keep a data structure representing our path from the prefix node to the current one. For this a stack’s push and pop functionality is exactly what we need, so we will use one.
Note how this approach still does not use constant memory, however we moved from memory linear in the size of the output, to linear in the length of the strings. For collections of many relatively short strings, this is a great improvement.
The implementation of this algorithm is fairly straight forward:
enumerateAllValues()
{
var stack = new Stack<Node>();
stack.Push(this);
while (stack.Count > 0)
{
var node = stack.Pop();
if (node.value != null)
yield return node.value;
if (node.children == null)
continue;
foreach (var child in node.children.Values)
stack.Pop(child);
}
}Using out data structure, this is the most efficient and clean solution possible. Unfortunately – by using an explicit stack, instead of an implicit call-stack – we add some bulk to our method which the recursive approach lacks.
The only thing that could tempt me to take another look at our recursive approach would be the addition of a yield foreach functionality to C#.
Extend prefix
Now that we have a list of all strings starting with a given prefix, we could use its result to find the longest shared prefix within that list. The result would be the longest unique extension of the original prefix, which can come in handy for things like typing suggestions and auto completion.
Instead of taking this long – and inefficient – route however, we can do much better by exploiting the properties of our data structure.
Notice how a node representing a longest common prefix is either a leaf, or has exactly two properties:
- it has no value itself;
- it has more than one child node.
If it does have a value, it trivially is itself the longest common prefix, since proceeding in its sub-trie would mean excluding itself.
Further, if it has only a single child node, the prefix of the current node, plus the character of the arc to its child is also a valid prefix, and it would be longer than the first one.
Using these two rules we can then find the longest common prefix we are looking for:
At first we again get the node of the given prefix using our very first method from above. Then we try to extend that prefix by walking through the tree until we find a node that conforms to our criteria and therefore is the node we are looking for. In the meantime we only have to keep track of all the characters we encounter and then return them as a string.
string extendPrefix(string prefix)
{
var node = this.getNode(prefix);
if (node == null)
return null;
return prefix + node.longestPrefixAddition();
}
string longestPrefixAddition()
{
var builder = new StringBuilder();
var node = this;
while (node.value == null && node.children.Count == 1)
{
var arc = node.children.First();
builder.Append(arc.Key);
node = pair.Value;
}
return builder.ToString();
}Note how I did not bother writing a recursive method in this case, even though it is entirely possible. I think that the iterative approach is clear enough, and to have good string building performance we need to use a StringBuilder in either case, which we would then have to hand down to the recursive call.
Conclusion
After implementing the construction of prefix-tries last week, we took a look at different methods of querying the data structure today.
I hope this has been interesting, or even useful to you.
As always, let me know what you think or if you have any questions in the comments below.
Enjoy the pixels!
| Reference: | Matching string prefixes using a prefix-trie 2 from our NCG partner Paul Scharf at the GameDev<T> blog. |